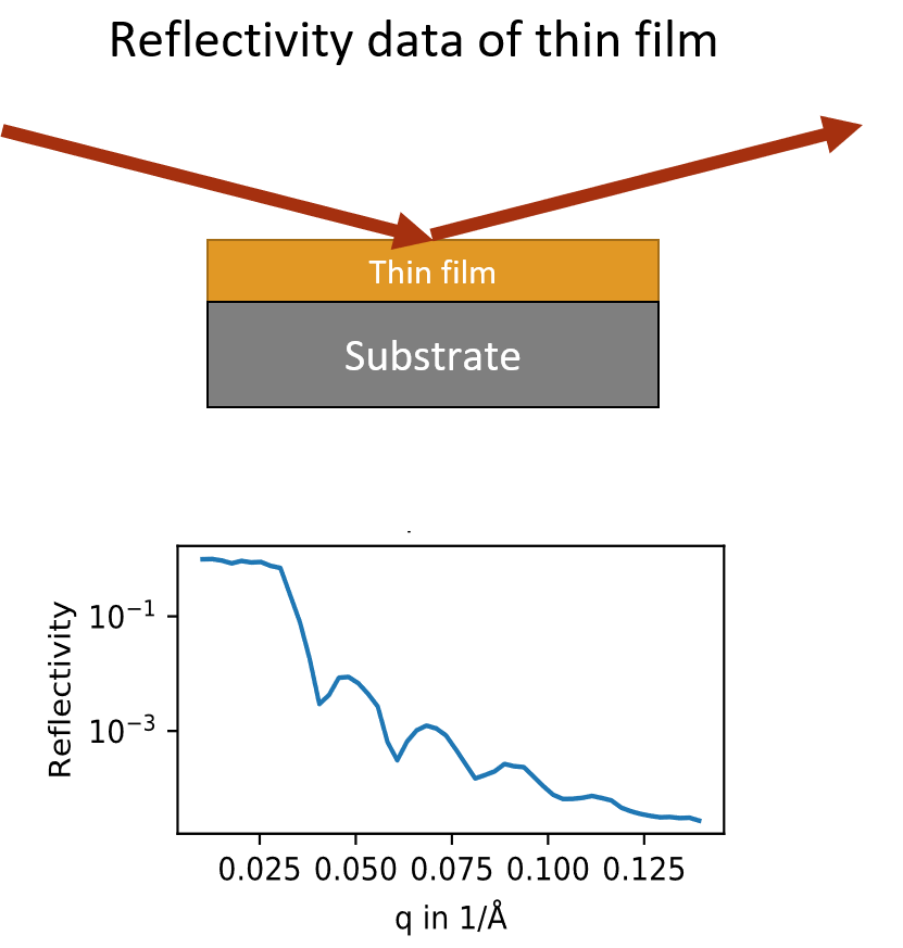
 X-ray reflectivity (XRR) is a
well-established analytical technique for thin film analysis. Reflectivity data provides information about the
scattering length density (SLD) as well as the thickness and interface roughness of thin films on an
Å-scale. XRR is commonly used for crystalline and amorphous films made by sputtering or molecular beam
deposition, but also for self-assembled monolayers and biological thin films. Furthermore, reflectivity
measurements can be performed in real time, which enables in situ studies of film growth.
However, thickness, roughness and SLD properties of thin films can generally not be extracted directly from
reflectivity data, but are instead refined during an iterative fitting process. Various programs are available
to accomplish this task by assuming a model for the sample geometry, calculating the resulting Fresnel
reflectivity via the Parratt algorithm or optical matrix formalism and iteratively varying the parameters until
a good fit is found. Even for a low number of layers, the parameter refinement is laborious and time
intensive. Furthermore, a good initial guess of the sample model is often necessary to ensure that the fit
converges to a global minimum.
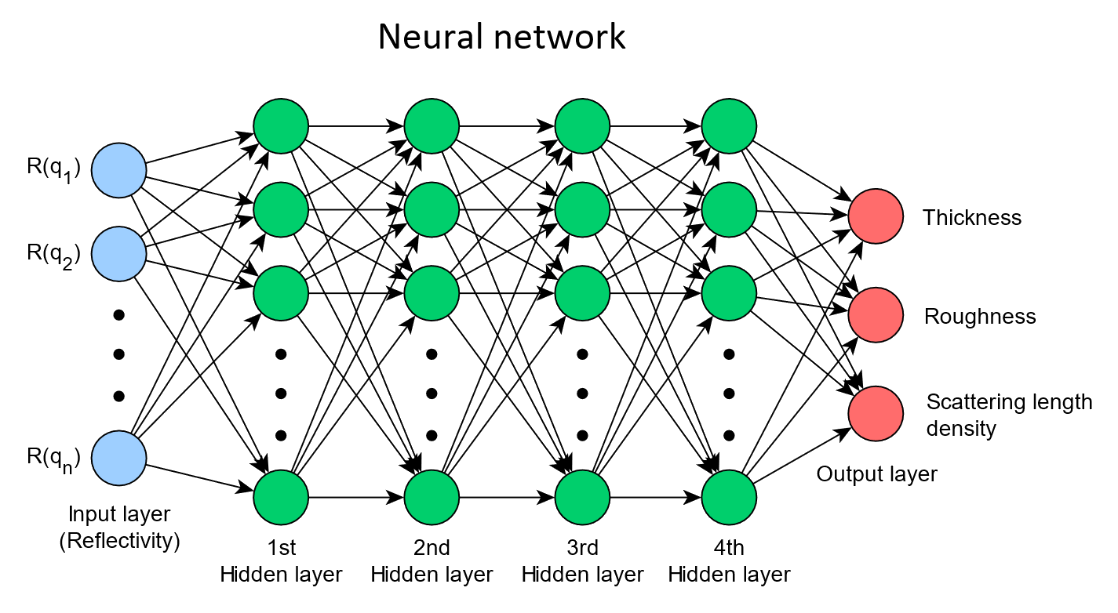
With artificial neural networks (ANNs) we can mitigate some of these drawbacks. By training a model with
simulated XRR data of many different thin films, we can create a neural network that is able to predict the
thickness, roughness and SLD by using experimentally measured XRR curves as input in less than 1 ms
[1]. However, the selection of the training data as well as the training procedure and model architecture are
critical aspects that govern the performance of the model. Therefore, most of the effort with this approach
flows into the refining these aspects.
For example, it is important to make sure that the simulated training data matches the experimental data as
closely as possible. Depending on the type of experiment, this can be a major challenge, especially if no
theoretical model is available. In the case of XRR, there are already good formalism (e.g. Parratt, Heavens)
that allow the modeling of mutlilayer thin film systems, but many experimental factors have to be taken into
account, such as resolution, noise and potential artifacts. However, once enough training data with a
sufficiently large parameter space is available for training, no further input is needed to determine film
properties from experimental data.
Another important aspect of machine learning is the choice of the model capacity. In general, a given model
should have a number of learnable parameters that corresponds to the complexity task that is to be solved. If
the model capacity is too low, it will not be able to find a good mapping between the input and output
regardless of the training process, which is called underfitting. If the model capacity is too large, it might
start learning details about the training data that are not present in data outside the training set. In this
case, the model will predict correct results on the data that was used for training, but not on new data, which
is called overfitting.
Lastly, the method by which the training of the model is carried out can also influence the prediction
performance. For example, the optimization algorithm for minimizing the training loss (a measure of progress
during training) can have significant impact on whether a global minimum is reached and training is
successful.
|
Recent progress in the field
of machine learning promises significant advances in scattering data analysis. For example, supervised learning
with artificial neural networks can be used to determine certain physical properties of molecular thin films by
using scattering data as input. After training, these machine learning models can yield results several orders
of magnitudes faster than conventional methods and generally do not require strict bounds or starting values, as
it is for example common for least mean square fitting.